Задачи с множествами

Множество - это совокупность объектов, которая рассматривается как единое целое и обладающих определенным свойством (признаком). Множество может быть ученники класса, фрукты, автомобили на парковке и т.д. В задачах ЕГЭ множествами являются сайты - результаты поисковых запросов в интернете.

Объекты, составляющие множество, называются элементами.

Множества принято обозначать латинскими буквами. Для наглядности множества представляют в виде окружностей, так называемых кругов Эйлера.

Пустым множество называется множество, которое не содержит элементы. Обозначается ∅.

Объединение. Объединение множеств A и B - это множество всех элементов, которые принадлежат хотя бы одному из множеств A или B. Обозначется A ∪ B. В языке запросов поисковых машин объединению соответствует знак | - или.

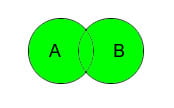
Пересечение. Пересечение множеств A и B - это множество элементов, которые принадлежат обоим множествам A и B. Обозначается A ∩ B. В языке запросов поисковых машин пересечению соответствует знак & - И.

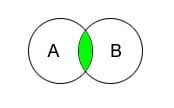
Разность. Разность множеств A и B - это множество элементов множества A, которые не принадлежат множеству B. Обозначается A \ B.

Мощностью множества называется число его элементов. Обозначается |A|

Для вычисления мощности объединения множеств имеет место быть формула (принцип включений и исключений):

|A ∪ B| = |A| + |B| - |A ∩ B|

Для вычисления мощности объединения трех множеств:

|A ∪ B ∪ C| = |A| + |B| + |C| - |A ∩ B| - |A ∩ C| - |B ∩ C| + |A ∩ B ∩ C|

Задача: В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

Запрос	Количество страниц (тыс.)
торты | пироги	12000
торты & пироги	6500
пироги	7700

Сколько страниц (в тысячах) будет найдено по запросу "торты"?

Решение: Обозначим буквой Т - множество страниц, отвечающих запросу "торты", а буквой П - отвечающих запросу "пироги". Тогда по формуле включений и исключений:

|Т | П| = |Т| + |П| - |Т & П|. Подставляем известные значения: 12000 = |Т| + 7700 - 6500, следовательно |Т| = 10800. Ответ: 10800

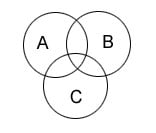
Задача: В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:

Запрос	Количество страниц (тыс.)
Толстой & Гоголь & Чехов	110
Гоголь & Чехов	275
Толстой & Чехов	215

Компьютер печатает количество страниц (в тысячах), которое будет найдено по следующему запросу: (Толстой|Гоголь) & Чехов Укажите целое число, которое напечатает компьютер. Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение: Представим множества страниц, найденных по запросам в виде кругов Эйлера. Каждую область пронумеруем, а мощность множества соответствующей области будем обозначать как N_i, где i - номер области (множества).

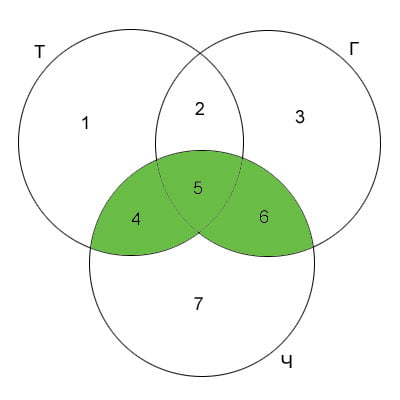
Тогда:

N₅ = 110

N₅ + N₆ = 275

N₄ + N₅ = 215

Интересующая нас область N₄ + N₅ + N_6.

Сложим второе и третье равентства: N₄ + 2N₅ + N₆ = 490, или N₄ + N₅ + N₆ = 490 - N₅ , подставим в правую часть известное нам значение N₅, N₄ + N₅ + N₆ = 380. Ответ: 380

Задачи для самостоятельного решения