Кодирование информации. Задача 3-12*
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, К решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 1; для буквы Б — кодовое слово 01. Какова наименьшая возможная сумма длин кодовых слов для букв В, Г, Д, Е, К?
Примечание: Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Построим дерево Фано для известных нам кодов букв А и Б:
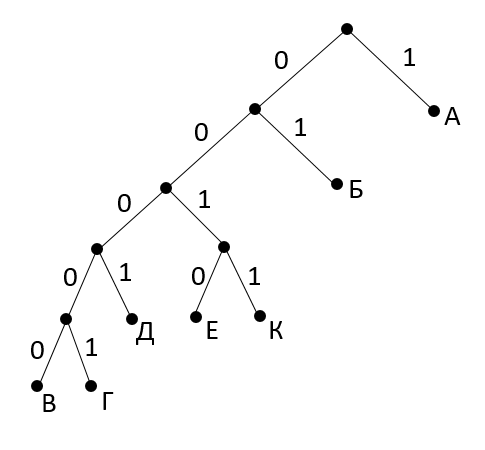
Свободную ветвь 00 будем равномерно наращивать, пока у нас не получится 5 конечных точек для букв В, Г, Д, Е, К. Запишем полученные кодовые слова:
В - 00000
Г - 00001
Д - 0001
Е - 0010
К - 0011
Сложим длины кодовых слов: 5 + 5 + 4 + 4 + 4 = 22.

