Алгебра логики. Задача 4-49
На числовой прямой даны два отрезка: P = [25, 37] и Q = [32, 50]. Отрезок A таков, что формула
(x ∈ A) → ((x ∈ P) ∨ (x ∈ Q))
тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Какова наибольшая возможная длина отрезка A?
Обозначим: (x ∈ A) как A, (x ∈ P) как P, (x ∈ Q) как Q и преобразуем выражение: \( A → (P + Q) = \overline{A} + P + Q \)
Отразим на числовой оси известные отрезки P и Q:
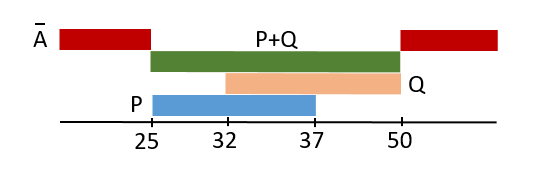
Чтобы выражение \( \overline{A} + P + Q \) было бы истинным при любом значении x, высказывание \( \overline{A} \) должно быть истинным, когда \( P + Q \) (зеленая область) ложно, поэтому высказывание \( A \) должно быть истинным, когда \( P + Q \) истинно. Из этого следует, что \( A \) может занимать любой отрезок в области \( P + Q \), но по условию задачи необходима наибольшая длина, поэтому он должен занимать всю область \( P + Q \), длина которой 50 - 25 = 25.

