Исполнители алгоритмов. Задача 9-1
Исполнитель Май17 преобразует число на экране, у него есть две команды, которым присвоены номера:
- Прибавить 1
- Прибавить 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Май17 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 17 и при этом траектория вычислений содержит число 9? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы.
Например, для программы 12 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12.
Для решения задачи составим таблицу, в которой в одном столбце число, а во втором- количество программ, которыми можно это число получить:
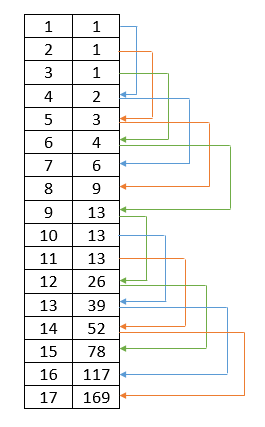
Также для вычисления количества программ n для очередного числа i можно воспользоваться формулой:
n(i) = n(i-1) + n(i-3) (если i-3 ≥ 1 и i-3 ≠ 7 и i-3 ≠ 8)
n(1) = 1
n(2) = n(1) = 1
n(3) = n(2) = 1
n(4) = n(3) + n(1) = 2
n(5) = n(4) + n(2) = 3
n(6) = n(5) + n(3) = 4
n(7) = n(6) + n(4) = 6
n(8) = n(7) + n(5) = 9
n(9) = n(8) + n(6) = 13
n(10) = n(9) = 13
n(11) = n(10) = 13
n(12) = n(11) + n(9) = 26
n(13) = n(12) + n(10) = 39
n(14) = n(13) + n(11) = 52
n(15) = n(14) + n(12) = 78
n(16) = n(15) + n(13) = 117
n(17) = n(16) + n(14) = 169

