Кнопка меню
ИНФОРМАТИКА
подготовка к ЕГЭ
  • Python
  • - Функции. Рекурсия
Задачи

Python. Функции. Рекурсия

Фрагмент программного кода, который используется в программе несколько раз, можно оформить в виде функции. Функции определяются в начале программы и могут принимать в качестве аргументов переменные. Функция может быть без аргументов и может не возвращать значения.

Для завершения работы функции используется инструкция return с указанием возвращаемого значения, которая обычно располагается в конце кода функции, но может быть указана и в середине кода. Инструкция return может указываться без значения или даже не присутствовать в функции, если возвращать значение нет необходимости.

Например, оформим вычисление факториала числа как функцию и с ее помощью выведем факториалы чисел 10 и 5:

def factorial(n):
    result = 1
    for i in range(n):
        result *= i + 1
    return result

print(factorial(10))
print(factorial(5))

В аргументе функции factorial передается число, факториал которого необходимо вычислить, в переменной result он вычисляется и возвращается инструкцией return. Тело функции оформлено блоком с отступом. Инструкции вывода основной программы расположены после описания функции.

Переменные, которые определены в теле функции (в нашем случае это result), доступны только в самой функции, основная программа к этим переменным не имеет доступа. В Python есть особенность использования переменных, которые определены в основном коде (так называемые глобальные переменные), они доступны внутри функции, если объявлены до ее вызова. Значение можно использовать для вычислений, но если внутри функции глобальной переменной будет присвоено любым оператором присвоение новое значение, то переменная перестанет быть глобальной и станет локальной внутри функции. Соответственно после возврата из функции в основном коде значение глобальной переменной останется неизменным.

Тип данных аргументов функции может быть любой, поэтому функция может по разному их обрабатывать. Например, функция вычисляет сумму двух переменных:

def add(a, b):
    return a + b

a = 1
b = 2
print(add(a, b))

Программа выведет 3 - сумму чисел 1 и 2, а если переменным присвоить строки:

def add(a, b):
    return a + b

a = '1'
b = '2'
print(add(a, b))

то программа выведет строку '12' - результат слияния строк a и b.

Рекурсия

В теле функций могут содержаться вызовы других функций, но, если функция вызывает сама себя, то такой вызов называтеся рекурсивным.

Следует понимать, что рекурсия - это способ организации цикла и чтобы он не был бы бесконечным, необходимо иметь возможность его закончить. Для этого в теле рекурсивной функии должно присутствовать условие с ветью, где вызова функции самой себя нет. Эта ветвь называется базовой, а ее условие - это условие завершения цикла.

Так как факториал числа n можно представить в виде выражения: n ⋅ (n - 1)!, напишем программу вычисления его вычисления с помощью рекурсивной функции:

def factorial(n):
    if n < 2:
        return 1
    else:
        return n * factorial(n - 1)

print(factorial(4))

Работает рекурсия следующим образом: если в теле функции встречается рекурсивный вызов, то значения всех переменных запоминаются в стеке, специально организованной памяти, а вызов передается вложенной функции с новыми аргументами и так до тех пор, пока в одном из рекурсивных вызовов не будет выполнено условие базовой ветви, после чего вызов будет возвращен на предыущий уровень и значения переменных будут восстановлены из стека. Затем вызов будет возвращен на уровень выше и т.д. до первого вызова.

Ниже представлена блок-схема рекурсивных вызовов вычисления функции factorial(4) в программе из примера:

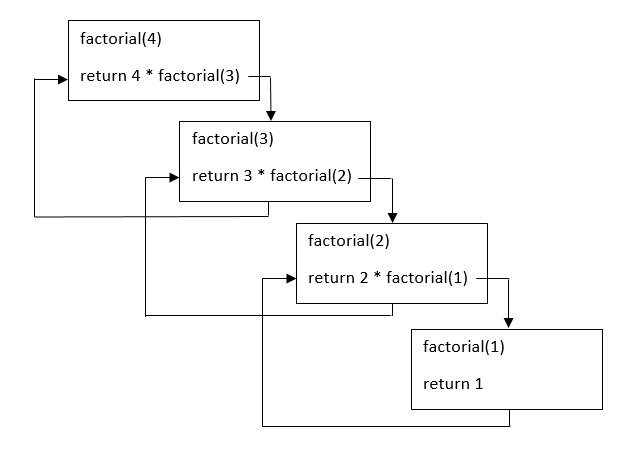
Блок-схема рекурсивных вызовов функции

Надо принять во внимание тот факт, что глубина стека, иначе говоря, количество рекурсивных вызовов ограничено. Если алгоритм задачи требует количество рекурсивных вызовов больше, чем заложено в реализации Python (порядка тысячи и более), интерпретатор выдаст ошибку.

Например, нам надо вывести последовательно все натуральные числа от 1 до n с помощью рекурсивной функции:

def sequence(n):
    if n > 1:
        sequence(n - 1)
    print(n)

sequence(5)

В этом примере печать начнется, когда вызов функции достигнет нижнего уровня при n = 1, а затем на каждом предыдущем уровне будет напечатана следующее число.

Если нам требуется вывести числа в обратном порядке, с n до 1, достаточно в функции инструкцию печати расположить до рекурсивного вызова:

def sequence(n):
    print(n)
    if n > 1:
        sequence(n - 1)

sequence(5)
 

Задачи для самостоятельного решения