Кодирование информации

Кодирование - это перевод информации в удобную форму для передачи, обработки и хранения с помощью некоторого кода. Обратный процесс называется декодированием.

Если все символы исходной информации кодируются кодами одинаковой длины, то кодирование называется равномерным. Если же используются коды разной длины, то кодирование называется неравномерным. В этом случае более часто встречающиеся символы обычно кодируют кодами меньшей длины, а для более редких - кодами большей длины.

Для неравномерного кодирования используется условие Фано: никакой код не должен быть началом другого кода. Если выполняется это условие, то гарантируется, что закодированное сообщение можно однозначно декодировать с начала.

Существует и обратное условие Фано: никакой код не должен быть окончанием другого кода. При этом условии гарантируется, что сообщение можно однозначно декодировать с конца.

Для решения задач, связанных с подбором неравномерных двоичных кодов удобно пользоваться наглядным способом - построением дерева Фано. Дерево строится по следующим правилам. Дерево строится начиная с начального узла - сверху вниз. Из любого узла, которое не закачивается сопоставленым символом выходят две ветви: левая, соответствующая нулю и правая, соответствующая единице. Код каждого символа получается записью нулей и единиц по кратчайшему пути с верхнего узла к с соответствующему символу.

Задача: В некотором сообщении используются только буквы А, Б, В, при этом чаще всего встречается буква А, а реже всего - буква В. Необходимо составить для этих букв коды наименьшей длины.

Решение: Строим дерево Фано.

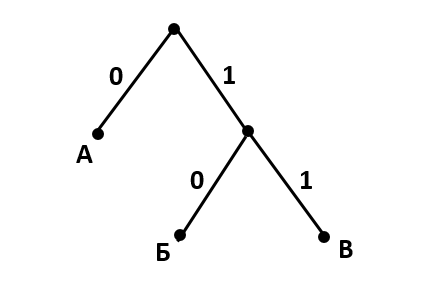
Так как буква А встречается чаще всего, чтобы код был наименьшей длины, ветвь 0 из вершины сразу завершаем этой буквой. Из узла ветви 1 строим ветви 0 и 1, которые завершаем буквами Б и В.

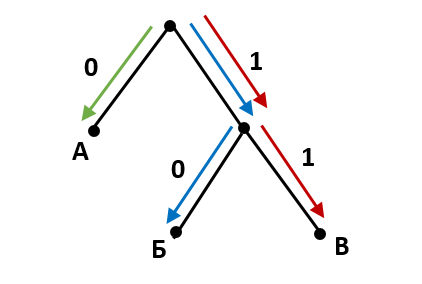
Записываем получившиеся коды: А - 0, Б - 10, В - 11

Кодирование текста

В ранних информационных системах использовалось восьмиразрядное кодирование символов, при котором каждому знаку препинания, цифрам и буквам английского языка ставилось в соответствие восьмиразрядное двоичное число (байт). Одним из примеров такой кодировки является кодировочная таблица ASCII. Кроме цифр, букв, знаков препинания, включая пробел (пустой промежуток между знаками), в этой таблице также присутствуют управляющие символы, например, невидимый символ перевода строки. Также в старшей половине таблицы присутствуют символы одного из национальных языков, например, русского. Так как байтом можно закодировать только 256 символов, то для кодирования различных языков применяются различные кодировочные таблицы.

В современных системах широкое распространение получила шестнадцатиразрядная кодировка Unicode. Младшие 128 кодов в этой кодировке соотвествуют таблице ASCII, а остальные коды предзначены для кодирования символов национальных языков.

Кодирование изображения

Возьмем к примеру небольшое черно-белое изображение:

Представим, что это изображение разлиновали вертикальными и горизонтальными линиями, иначе говоря, наложили на нее мелкую сетку (растр):

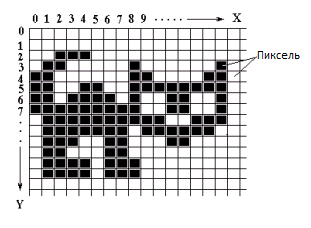
То есть, у нас получилось мозаика из черных и белых квадратиков, называемых пикселями. Пиксель - термин, образованный сокращением фразы picture element. Если поставить в соответствие черному пикселю 0, а белому - 1 , то можно закодировать это изображение, записав подряд все нули и единицы, соответствующие пикселям этого изображения. Такой способ кодирования изображения называется растровым.

Если для пикселя использовать не один бит, а восемь, то можно закодировать цветное изображение, где каждый пиксель, может быть окрашен в один из 256 цветов. Количество бит, предусмотренных для пикселя называется глубиной цвета. А ширина и высота изображения в пикселях - разрешающей способностью.

В современных компьютерных системах для пикселя отводят 3 байта, один байт для каждого из основных цветов: красного, зеленого и синего. То есть 24 бита обеспечивают представление 2²⁴ = 16 777 216 цветов.

Для того, чтобы рассчитать количество бит, необходимых для кодирования изображения, нужно умножить глубину цвета (количество бит пикселя) на ширину и высоту изображения в пикселях.

Задача: Какой объем видеопамяти в байтах требуется для хранения растрового изображения, занимающего весь экран монитора с разрешающей способностью 640×480 пикселей, если используется палитра из 65536 цветов?

Решение: Глубина цвета составляет log₂65536 = 16 бит. Следовательно для хранения одно пикселя требуется 2 байта. Объем видеопамяти: 640 ⋅ 480 ⋅ 2 = 614400 байт.

Кодирование звуковой информации

Чтобы закодировать звуковой сигнал производят его дискретизацию по времени, что означает измерение его амплитуды через равные промежутки времени. Представим график звукового сигнала, в котором по горизонтальной оси отложено время, а по вертикальной - амплитуда в условных единицах в диапазоне от -1 до 1:

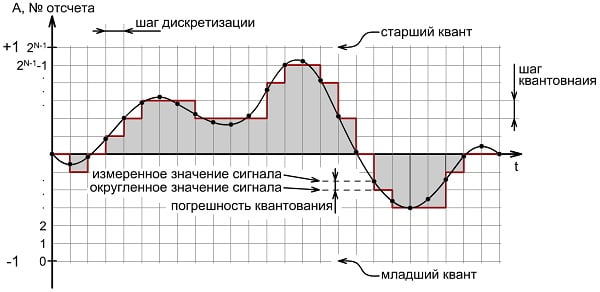
Частота, с которой производится измерение сигнала, называется частотой дискретизации. Для качественного кодирования по теореме Найквиста эта частота должна быть в два раза выше частоты кодируемого сигнала. Так как человек слышит звук частотой до 20 кГц, то достаточно кодировать его частотой свыше 40 кГц. К примеру, на компакт-дисках применяется частота дискретизации 44 кГц, а для человеческого голоса при кодировании для передачи по каналам связи достаточно 8 кГЦ.

Для каждого отсчета при измерения амплитуды сигнала применяется его квантование, то есть значению амплитуды ставится в соответствие стандартный уровень в зависимости от того, какое количество этих уровней (шагов квантования) выбрано. Количество бит, необходимых для обеспечения квантования называется глубиной кодирования. Естественно, что квантование производится с некоторой погрешностью, но она тем ниже, чем больше глубина кодирования.

Итак, частота дискретизации при кодировании означает количество отсчетов в секунду. Частота 44 кГц - это 44000 отсчетов в секунду. Чтобы вычислить объем информации в битах, необходимый для кодирования звукового сигнала нужно частоту дискретизации умножить на глубину кодирования и на количество секунд, в течении которого сигнал кодируется. Если каналов звукового сигнала больше чем один, то полученный объем надо умножить еще и на количество каналов, например, на 2 при стерео-звуке.

Задача: Сколько байтов требуется для кодирования 1 минуты речи с частотой дискретизации 8 кГц и глубиной кодирования 10 бит.

Решение: Так как в минуте 60 секунд, то требуемый объем 8000 ⋅ 60 ⋅ 10 = 4800000 бит. Делим на 8, получаем 600000 байтов.

Скорость передачи информации

Каналы связи для передачи информации имеют ограничение скорости (пропускную способность). Это ограничение связано с физическими свойствами аппаратуры.

Зная пропускную способность канала можно вычислить объем передаваемой информации за какое-то время.

Задача: Скорость передачи данных (пропускная способность) через ADSL─соединение равна 64000 бит/c. Передача файла через это соединение заняла 30 секунд. Определить размер файла в байтах.

Решение: 640000 ⋅ 30 = 1920000 бит. переведем в байты, 1920000 : 8 = 240000 байт.

Задачи для самостоятельного решения

• Задача 3-1
  Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 10. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
• Задача 3-2
  Для кодирования некоторой последовательности, состоящей из букв И, К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 10. Какова наименьшая возможная суммарная длина всех пяти кодовых слов?
• Задача 3-3
  По каналу связи передаются сообщения, содержащие только четыре буквы: П, О, С, Т; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, П используются такие кодовые слова: Т: 111, О: 0, П: 100. Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
• Задача 3-4*
  По каналу связи передаются сообщения, содержащие только четыре буквы: А, Б, В, Г; для передачи используется двоичный код, удовлетворяющий условию Фано. Для букв Б, В, Г используются такие кодовые слова: Б — 101; В — 110; Г — 0. Укажите кратчайшее кодовое слово для буквы А, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наибольшим числовым значением.
• Задача 3-5*
  Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали кодовые слова 100, 101, 00, 01 соответственно. Для двух оставшихся букв — Д и Е — коды неизвестны.
  Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
• Задача 3-6*
  В сообщении встречается 10 разных букв. При его передаче использован неравномерный двоичный префиксный код. Известны коды трех букв: 11, 100, 101. Коды остальных семи букв имеют одинаковую длину. Какова минимальная суммарная длина всех 10 кодовых слов?
• Задача 3-7*
  В сообщении встречается 7 разных букв. При его передаче использован неравномерный двоичный код, удовлетворяющий условию Фано. Известны коды трёх букв: 1, 01, 001. Коды остальных четырёх букв имеют одинаковую длину. Какова минимальная суммарная длина всех семи кодовых слов?
• Задача 3-8*
  По каналу связи передаются шифрованные сообщения, содержащие только пять букв: А, Б, В, Г, Д. Для передачи используется неравномерный двоичный код. Для букв А, Б и В используются кодовые слова 1100, 1110, 11010 соответственно. Укажите минимальную сумму длин кодовых слов для букв Г и Д, при котором код будет удовлетворять условию Фано. Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
• Задача 3-9*
  По каналу связи с помощью равномерного двоичного кода передаются сообщения, содержащие только 4 буквы Г, О, Р, Б. Каждой букве соответствует своё кодовое слово, при этом для набора кодовых слов выполнено такое свойство: любые два слова из набора отличаются не менее чем в трёх позициях. Это свойство важно для расшифровки сообщений при наличии помех. Для кодирования букв Г, О, Р используются 5-битовые кодовые слова: Г - 11000, О - 01111, Р - 10110 Определите кодовое слово для буквы Б, если известно 5-битовый код для буквы Б начинается с 0 и заканчивается на 1.
• Задача 3-10*
  Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Если таким способом закодировать последовательность символов ГВББАГ и записать результат восьмеричным кодом, то получится 6413 8. Запишите в качестве ответа, какой код соответствует букве В.
• Задача 3-11*
  По каналу связи с помощью равномерного двоичного кода передаются сообщения, содержащие только 4 буквы К, И, П, Р. Определите суммарную длину всех кодовых слов, если известно, что все буквы имеют равномерный код.
• Задача 3-12*
  Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, К решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 1; для буквы Б — кодовое слово 01. Какова наименьшая возможная сумма длин кодовых слов для букв В, Г, Д, Е, К?
• Задача 3-13
  Для хранения растрового изображения размером 160×128 пикселей отвели 5 Кбайт памяти. Каково максимально возможное количество цветов в палитре изображения?
• Задача 3-14
  Для хранения растрового изображения размером 32×32 пикселей отвели 512 байт памяти. Каково максимально возможное количество цветов в палитре изображения?
• Задача 3-15
  Какой объем памяти в байтах необходимо выделить под хранение растрового изображения размером 128 х 128 пикселей, если в палитре 64 цвета?
• Задача 3-16
  Скорость передачи данных через ADSL-соединение равна 2 500 000 бит/с. Через данное соединение передают файл размером 10 Мбайт. Определите время передачи файла в секундах, (Служебной информацией пренебречь).
• Задача 3-17
• Задача 3-18
  Сколько секунд потребуется модему, передающему информацию со скоростью 9600 бит/с, чтобы передать 70 страниц текста в 60 строк по 75 символов каждая при условии, что каждый символ кодируется двумя байтами. Результат представьте целым числом. (Служебной информацией пренебречь).
• Задача 3-19
  Сколько секунд потребуется модему, передающему информацию со скоростью 9600 бит/с, чтобы передать цветное растровое изображение размером 1024×768 пикселей при условии, что в палитре 16 цветов. Результат представьте целым числом. (Служебной информацией пренебречь).
• Задача 3-20*
  Автоматическая камера производит растровые изображения размером 512×1024 пикселей. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Объём файла с изображением не может превышать 260 Кбайт без учёта размера заголовка файла. Какое максимальное количество цветов можно использовать в палитре?
• Задача 3-21*
  Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 75 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 3 раза выше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 90 секунд. Во сколько раз скорость пропускная способность канала в город Б больше пропускной способности канала в город А?
• Задача 3-22*
  Для хранения одноканальной (моно) звукозаписи с частотой дискретизации 24 кГц и глубиной звука 16 бит выделено 375 Кбайт памяти. Сжатие данных не производится. Какова продолжительность звукозаписи в секундах? Ответ запишите без указания единиц измерения.
• Задача 3-23*
  Светлана сделала аудиозапись доклада своей одноклассницы и хочет переслать полученный файл по Wi-Fi-каналу связи. Параметры аудиозаписи: режим записи — стерео (двухканальная), частота дискретизации — 16 кГц, число уровней квантования сигнала — 65536, длительность записи — 8 минут. При записи данных в файл сжатие данных не производилось. Известно, что максимально возможная скорость передачи данных по имеющемуся в наличии Светланы каналу связи составляет 10 Мбит в секунду. Определите, какое минимальное количество секунд может потребоваться Светлане для передачи файла. В ответе укажите целое число секунд.
• Задача 3-24*
  Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 96 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 4 раза выше и частотой дискретизации в 3 раза ниже, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 16 секунд. Во сколько раз скорость пропускная способность канала в город Б больше пропускной способности канала в город А?
• Задача 3-25*
  Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 30 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б; пропускная способность канала связи с городом Б в 4 раза выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б? В ответе запишите только целое число, единицу измерения писать не нужно.
• Задача 3-26*
  Производилась двухканальная (стерео) звукозапись с частотой дискретизации 64 кГц и 24-битным разрешением. В результате был получен файл размером 120 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) производилась запись. В качестве ответа укажите ближайшее к времени записи целое число, кратное 5.