Алгебра логики. Задача 4-52*
На числовой прямой даны два отрезка: P = [5, 13] и Q = [12, 19]. Укажите наибольшую возможную длину промежутка A, для которого формула
((x ∈ P) ≡ (x ∈ Q)) → ¬(x ∈ A)
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
Ответ
7
Решение
Обозначим: (x ∈ A) как A, (x ∈ P) как P, (x ∈ Q) как Q и преобразуем выражение: \( (P ≡ Q) → \overline{A} = \overline{(P ≡ Q)} + \overline{A} \)
Выражение \( \overline{(P ≡ Q)} \) истинно тогда, когда x ∈ [5, 12] и x ∈ [13, 19]:
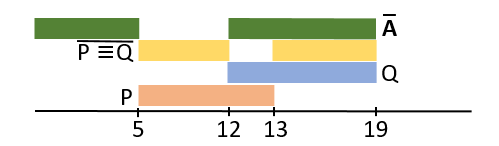
Чтобы выражение \( \overline{(P ≡ Q)} + \overline{A} \) было истинно при любом значении x, A должно лежать или в промежутке [5, 12] или - в [13, 19]. Следовательно наибольшая длина отрезка A: 12 - 5 = 7.

