Алгебра логики. Задача 4-51*
Даны три отрезка на числовой прямой: A = [5, 12], B = [13, 19], C = [4,Y]. Какому минимальному целому числу может быть равен Y, чтобы выражение выполнялось для любого x? (x ∉ C) → ((X ∈ B) →(x ∈ A)) = 1
Обозначим: (x ∈ A) как A, (x ∈ B) как B, (x ∈ C) как C и преобразуем выражение: \( \overline{C} → (B → A) = \overline{C} → (\overline{B} + A) \) \( = C + \overline{B} + A \)
Обозначим: (x ∈ A) как A, (x ∈ B) как B, (x ∈ C) как C и преобразуем выражение: \( \overline{C} → (B → A) = \overline{C} → (\overline{B} + A) \) \( = C + \overline{B} + A \)
Отразим на числовой оси области \( A \) и \( \overline{B} \):
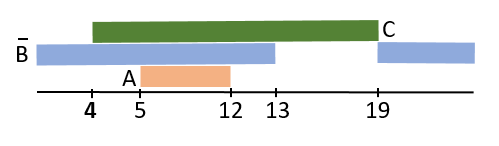
Заметим, что область \( \overline{B} \) включает в себя область \( A \) , поэтому последнюю можно не рассматривать. Чтобы выражение \( C + \overline{B} \) было бы истинным при любом значении x, высказывание \( С \) должно быть истинным, когда \( \overline{B} \) ложно. Из этого следует, что отрезок \( С \) должен заканчиваться, как минимум, в точке 19, поэтому его длина 19 - 4 = 15.

