Кнопка меню
ИНФОРМАТИКА
подготовка к ЕГЭ
  • Pascal
  • - Процедуры и функции
Задачи

Pascal. Процедуры и функции

Логически завершенные фрагменты кода, которые используются в программе несколько раз, удобно оформлять в виде функций или процедур, которые описываются в начале программы, до блока объявления переменных. Если в результате работы фрагмента кода надо вернуть какое-то значение, то используется функция. Если возвращать ничего не нужно (например, фрагмент используется для печати) или нужно возвращать несколько значений - используется процедура.

Например, в программе нам необходимо вычислить факториал чисел 5 и 10. Напишем функцию, которая будет вычислять и возвращать факториал числа, переданному в аргументе:

function factorial(n : integer) : integer;
var
  i, f : integer;
begin
  f := 1;
  for i := 2 to n do
    f := f * i;
  factorial := f;
end;

begin
  Writeln('Факториал 5: ', factorial (5));
  Writeln('Факториал 10: ', factorial (10));
end.

Обратите внимание, что при определении функции мы не только определяем тип аргумента, но и определяем тип возвращаемого функцией значения. В конце вычислений полученное значение присваивается функции по ее имени. Также присвоить значение функции можно, если вместо имени использовать ключевое слово result.

Если перед аргументом в описании функции или процедуры указать ключевое слово var, то в функцию или процедуру будет передано не само значение , а ссылка на переменную, поэтому все мзменения этой переменной в функции останутся после возврата в основную программу. Для передачи ссылок на массивы и другие структуры данных необходимо описать их в блоке type. Например, напишем процедуру определения максимального значения в массиве:

type
  array10 = array[1..10] of integer;
procedure max_element(var massiv: array10; var maxval : integer);
var
  i, f : integer;
begin
  maxval := 0;
  for i := 1 to 10 do
    if massiv[i] > maxval then
      maxval := massiv[i];
end;

var
  maxval :integer;
  massiv : array10 = (2, 1, 15, 7, 4, 12, 11 , 9, 14, 3);
begin
  max_element(massiv, maxval);
  Writeln('Максимальное значение: ', maxval);
end.

Рекурсивные функции и процедуры

Если в теле функции или процедуры используется вызов самой себя, то она называется рекурсивной. Чтобы рекурсивная функция не вызывала бы себя бесконечно, в ней обязательно должна быть базовая ветвь, где вызова самой себя нет. Следует понимать, что рекурсия - это один из способов организации цикла, условием прекращения которого является базовая ветвь рекурсивной функции.

Исходя из выражения n! = n ⋅ (n - 1)!, напишем рекурсивную функцию вычисления факториала числа:

function factorial(n : integer) : integer;
begin
  if n < 2 then
    factorial := 1
  else
    factorial := n * factorial(n-1);
end;

begin
  Writeln('Факториал 5: ', factorial(5));
  Writeln('Факториал 10: ', factorial(10));
end.

Механизм рекурсии работает следующим образом: если в теле функции встречается рекурсивное обращение к самой себе, то все текущие значения переменных сохраняются в специальной памяти, называемой стеком, после чего управление передается вызову функции с уже новыми значениями переменных. Это происходит до тех пор, пока в текущем вызове не будет выполнена базовая ветвь и управление будет возвращено на предыдущий уровень, будут восстановлены значения переменных из стека, а затем управление будет передано на уровень, предшествущий предыдущему и т.д., пока управление не вернется в точку первого вызова функции.

На нижеследующем рисунке представлена схема вызовов рекурсивной функции factorial(5):

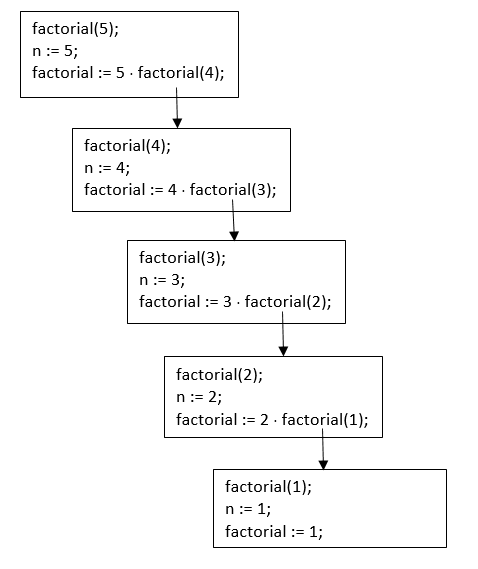
Рекурсивный вызов функции

 

Задачи для самостоятельного решения