Алгебра логики. Задача 4-56
Известно, что для некоторого отрезка А формула
((x ∈ A) → (x2 ≤ 81)) ∧ ((x2 ≤ 64) → (x ∈ A))
тождественно истинна (то есть принимает значение 1 при всех вещественных значениях переменной x). Какую наибольшую длину может иметь отрезок A?
Преобразуем выражение: \( ((x ∈ A) → (x^2 ≤ 81)) ⋅ ((x^2 ≤ 64) → (x ∈ A)) = \) \( ((x ∉ A) + (x^2 ≤ 81)) ⋅ ((x^2 > 64) + (x ∈ A)) \)
Чтобы это выражение было истинно, необходимо, чтобы истинны были оба члена конъюнкции, поэтому:
\( \begin{cases} (x ∉ A) + (x^2 ≤ 81) = 1 \\ (x^2 > 64) + (x ∈ A) = 1 \end{cases} \)
В первом уравнении системы, чтобы выражение было истинно, достаточно, чтобы истинным был один из членов дизъюнкции, поэтому \( (x ∉ A) \) должно быть истинно при \( (x^2 > 81) \) или \( (x < -9) \), \( (x > 9) \).
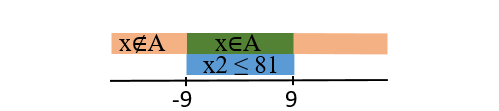
Следовательно, A при x ∈ [-9,9].
Во втором уравнении системы, чтобы выражение было истинно, достаточно, чтобы истинным был один из членов дизъюнкции, поэтому \( (x ∈ A) \) должно быть истинно при \( (x^2 ≤ 64) \) или \( (x > -8) \), \( (x < 8) \).
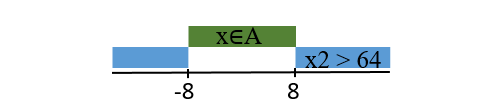
Следовательно, A при x ∈ [-8,8]. Так как отрезок x ∈ [-9,9] включает в себя отрезок x ∈ [-8,8], то наибольшая длина: 9 + 9 = 18

