Алгебра логики. Задача 4-53
Для какого наименьшего целого числа А формула
((x < 5) → (x⋅x ≤ A)) ∧ ((y⋅y ≤ A) → (y ≤ 7))
тождественно истинна (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?
Преобразуем выражение: \( ((x < 5) → (x^2 ≤ A)) ⋅ ((y^2 ≤ A) → (y ≤ 7)) = \) \( ((x ≥ 5) + (x^2 ≤ A)) ⋅ ((y^2 > A) + (y ≤ 7)) \)
Чтобы это выражение было истинно, необходимо, чтобы истинны были оба члена конъюнкции, поэтому:
\( \begin{cases} (x ≥ 5) + (x^2 ≤ A) = 1 \\ (y^2 > A) + (y ≤ 7) = 1 \end{cases} \)
В первом уравнении системы, чтобы выражение было истинно, достаточно, чтобы истинным был один из членов дизъюнкции, поэтому \( (x^2 ≤ A) \) должно быть истинно при \( (x < 5) \). Подставляя \( (x = 4) \) в \( (x^2 ≤ A) \), получим \( (A ≥ 16) \). Проиллюстрируем графически:
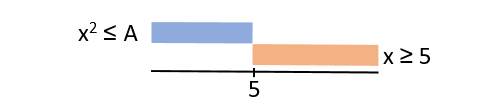
Аналогично рассуждая: \( (y > 7) \), подставляя \( (y = 8) \) в \( (y^2 > A) \), получим \( (A < 64) \). То есть:
\( \begin{cases} A ≥ 16 \\ A < 64 \end{cases} \)
Наименьшее целое число, удовлетворяющее системе \( A = 16 \)

