Исполнители алгоритмов. Задача 9-6
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 5 камней; такую позицию в игре будем обозначать (10, 5). Тогда за один ход можно получить любую из четырёх позиций: (11, 5), (20, 5), (10, 6), (10, 10). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней.
В начальный момент в первой куче было семь камней, во второй куче — S камней; 1 ≤ S ≤ 69.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т. е. не являющиеся выигрышными независимо от игры противника.
а. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна
б. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
- Петя не может выиграть за один ход;
- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
в. Найдите минимальное значение S, при котором одновременно выполняются два условия:
- у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
- у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Найденные значения в пунктах а, б, в, укажите как строку с числами, без разделителей.
а. Так как минимальное значение количества камней, когда игра заканчивается, в обеих кучах равнв 77, а в первой уже 7, то во второй куче должно быть 70, чтобы игра окончилась за один ход Вани. Минимальное значение количества камней во второй куче должно быть равно 35, чтобы Ваня смог бы его удвоить для выигрыша. А минимальное количество камней во второй куче должно быть 18, чтобы Петя своим ходом, удвоив ее, смог бы достичь 35. Ответ:18.
б. Чтобы Петя не смог бы выиграть за один ход, во второй куче должно быть не более 34 камней, потому что 35 камней - это минимальное количество камней, при котором можно выиграть одним ходом. Поэтому проверим позицию (7, 34). В этой позиции Пете достаточно для выигрыша положить в первую кучу один камень (8, 34), потому что при любом ходе Вани, следующим ходом Петя удваивает количество камней во второй куче. Первое число 34.
Предположим, что в первой куче оказалось 14 камней после выигрышного хода Пети. Тогда во второй куче должно было бы быть 63 камня, как минимум. Следовательно, в начальной позиции во второй куче должно быть не более 31 камня, чтобы Ваня не смог бы выиграть первым ходом. Проверим начальную позицию (7, 31):
Петя делает первый ход (14, 31). После хода Вани могут возникнуть позиции: (15, 31), (28, 31), (14, 32), (14, 64). В любом случае Петя удваивает количество камней во второй куче и выигрывает. Второе число: 31.
Ответ: 3134
в. В пункте б выяснилось, что позиция (7, 31) выигрышная для первого игрока, поэтому предположим, что нужная начальная выигрышная позиция для Вани (7, 30). После первого хода Пети могут возникнуть позиции: (8, 30), (14, 30), (7, 31), (7, 60). Представим дерево игры в виде таблицы:
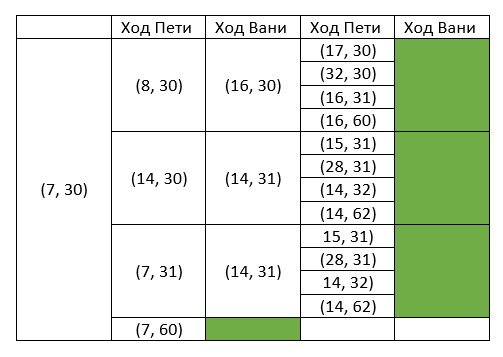
Как видно из таблицы, для каждой позиции после хода Пети у Вани есть выигрышная стратегия, в которой он последним ходом удваивает количество камней во второй куче.
Ответ: 30

