Алгебра логики. Задача 4-58

Чтобы значение дизъюнкции \( (y - 2x < A) + (x > 20) + (y > 20) \) было бы истинно, необходимо, чтобы выражение \( y - 2x < A \) было истинно, когда выражения \( x > 20 \) и \( y > 20 \) ложны, т.е \( x ≤ 20 \) и \( y ≤ 20 \). Кроме того, по условиям задачи \( x > 0 \) и \(y > 0 \) , так как рассматриваются только целые положительные значения \(x\) и \(y\), поэтому область \( (x ≤ 20)⋅(y ≤ 20)⋅(x > 0)⋅(y > 0) \) должна быть включена в область, расположенную ниже прямой \( y = 2x + A \):

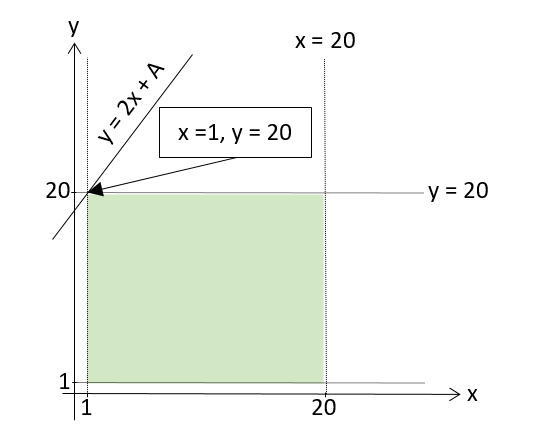
Следовательно прямая \( y = 2x + A \) должна проходить не ниже точки \( x = 1, y = 20 \). Подставим эти значения в выражение \( y - 2x < A \):

\( 20 - 2 ⋅ 1 < A ⇒ A > 18 \). Ответ: 19