Моделирование и компьютерный эксперимент
В задачах данного раздела используются табличный и графический способы представления информации. Задачи могут быть связаны с переводом представления данных из одного вида в другой.
Задача: В таблице приведена стоимость перевозок между соседними станциями. Укажите схему, соответствующую таблице.
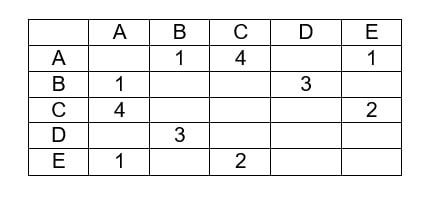
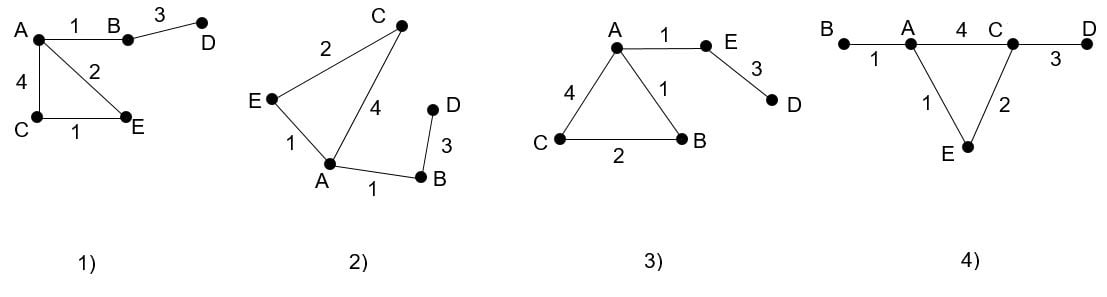
Решение: Точками обозначены станции (в таблице - латинские буквы), а отрезками - стоимость перевозки. Если стоимость в таблице не указана, то между станциями нет сообщения. Эту задачу лучше решать методом исключения.
В соответствии с таблицей станция A соединена со станциями B, C, E. Все варианты схем соотвествуют этому, но в варианте 1 для отрезка AE указана стоимость 2, а по таблице должна быть 1.
В соответствии с таблицей станция B соединена со станциями A и D. На схемах 3 и 4 точка B не соединяется с точкой D.
Остается только проверить, что схема 2 соответствует остальным строкам таблицы. Ответ: 2
Задача: На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
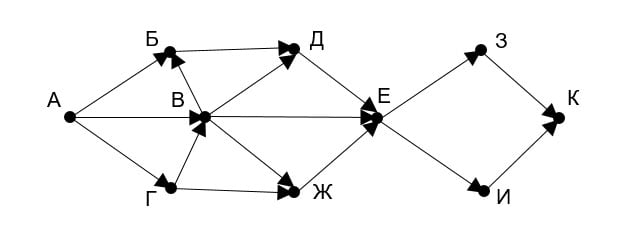
Решение: Начнем считать количество путей с начала маршрута - с города А, приняв за начальный отсчет количество путей, приведших в этот город равным 1.
А = 1
Следующим городом, для которого можно подсчитать пути будет Г, потому что к нему идет только один путь из города А:
Г = 1
Для города В два пути, по которым можно в него попасть - А и Г. Суммируем пути города А и пути города Г:
В = А + Г = 1 + 1 = 2
Далее для города Б:
Б = А + В = 1 + 2 = 3
Аналогично, последовательно подсчитываем количество путей для остальных городов:
Д = Б + В = 3 + 2 = 5
Ж = В + Г = 2 + 1 = 3
Е = Д + В + Ж = 5 + 2 + 3 = 10
З = Е = 10
И = Е = 10
К = З + И = 10 + 10 = 20
Удобней, все расчеты вести на самой схеме:
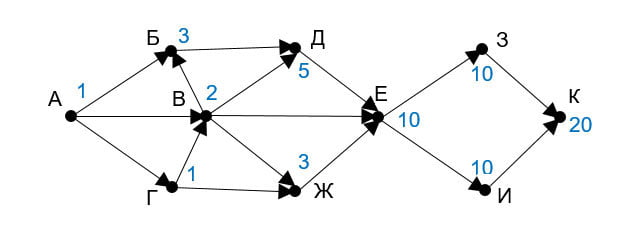
Ответ: 20

