Кнопка меню
ИНФОРМАТИКА
подготовка к ЕГЭ
Задачи

Исполнители алгоритмов

Задача: У исполнителя Калькулятор две команды, которым присвоены номера:

  1. вычти 1;
  2. умножь на 3;

Первая из них уменьшает число на экране на 1, вторая увеличивает его в 3 раза. Запишите порядок команд в программе получения из 4 числа 17, содержащей не более 5 команд, указывая лишь номера команд.

Например, 12211 - программа:

которая преобразует число 2 в 17.

Если таких программ более одной, то запишите любую из них.

Решение: Поиск программы лучше начать с конца - результата выполнения программы. 17 не делиться на 3, но ближайшее большее число 18 - делится. Следовательно последняя команда в программе будет 1. Число 18 можно получить умножив 6 на 3, число 6 - умножив 2 на 3, следовательно последние три команды программы - 221. Число 2 можно получить, если дважды вычесть 1 из исходного числа 4, Вся программа будет выглядеть: 11221. Программа содержит 5 команд - условие задачи выполнено. Ответ: 11221

Задача: У исполнителя Утроитель две команды, которым присвоены номера:

  1. прибавь 1;
  2. умножь на 3;

Первая из них увеличивает число на экране на 1, вторая увеличивает его в 3 раза. Сколько есть программ, которые число 1 преобразуют в число 23?

Решение: Для решения задачи составим таблицу, в которой в одном столбце число, а во втором- количество программ, которыми можно это число получить:

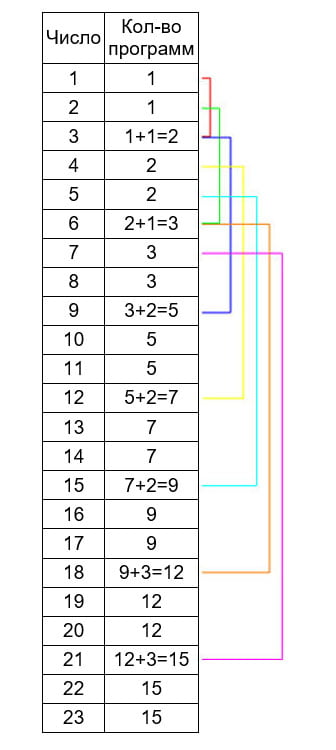
Таблица количества программ

Ответ: 15

Задача: Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существуют две команды:

Вперед n, где n - целое число, вызывающая передвижение черепашеки на n шагов в направлении движения;

Направо m, где m - целое число, вызывающая изменение направления движения на m градусов по часовой стрелке.

Запись Повтори 5 [Команда1 Команда2] означает, что последовательность команд в скобках повторится 5 раз. Исполнитель интерпретирует эту запись как одну команду.

Черепашке был дан для исполнения следующий алгоритм:

Повтори 5 [Повтори 2 [Вперед 40 Направо 60 Вперед 40 Направо 120] Направо 90]

Какая фигура появится на экране?

Варианты ответа

Решение: В результате исполнения внутреннего цикла черепашка рисует ромб, так как за один шаг она рисует две линии одинаковой длины, при этом поворачивается на 180 градусов. За второй шаг рисуются линии в обратном направлении. Согласно внешнему циклу черепашка рисует ромб пять раз, при этом за 4 шага она поворачивается на 360 градусов, а пятый ромб будет нарисован поверх первого. Ответ: 3

Задача: Исполнитель Робот действует на клетчатой доске, между соседними клетками которой могут стоять стены. Робот передвигается по клеткам доски и может выполнять команды 1 (вверх), 2 (ввниз), 3 (вправо), 4 (влево), переходя на соседнюю клетку в направлении, указанном в скобках. Если в этом направлении между клетками стоит стена, то Робот разрушается. Робот успешно выполнил программу

11313142

Какую последовательность из четырех команд должен выполнить Робот, чтобы вернуться в ту клетку, где он был перед началом выполнения программы и не разрушиться вне зависимости от того, какие стены стоят на поле?

Решение: Отразим путь, который проделал Робот, графически:

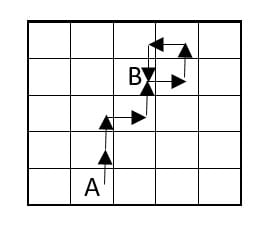
Путь робота

Буквой A обозначим клетку, в которой находился Робот до выполнения программы, а буквой B - клетку, в которой оказался после. Из рисунка видно, что вернуться из точки B в точку A можно по прорамме: вниз, влево, вниз, вниз, то есть 2422. Ответ: 2422

Задача: Дана система команд исполнителя, "живущего" в прямоугольном лабиринте на клетчатой плоскости.

Поле для робота

При выполнении любой из команд: вверх, вниз, влево, вправо Робот перемещается на соответствующую клетку,

Команды проверки истинности условия на наличие стены у той клетки, где он находится:

сверху свободно

снизу свободно

слева свободно

справа свободно

Если Робот начнет движение в сторону стены, то он разрушится.

Сколько клеток данного лабиринта соответствуют требованию, что, выполнив предложенную программу, Робот остановится в той же клетке, с которой начал движение?

НАЧАЛО

ПОКА справа свободно ДЕЛАТЬ вправо

ПОКА снизу свободно ДЕЛАТЬ ввниз

ПОКА слева свободно ДЕЛАТЬ влево

ПОКА сверху свободно ДЕЛАТЬ вверх

КОНЕЦ

В ответе запишите число - количество таких клеток, а далее, через запятые, их адреса (сначала латинская буква столбца, а затем цифра строки, например, нижний левый угол лабиринта имеет адрес A1).

Решение: Согласно последнему циклу программы Робот должен остановится в клетке, которая ограничена стеной сверху, при этом в лабиринте он должен описать прямоугольник. Проверяем все такие клетки: клетки верхнего ряда, B6, H6, C5, D4, E2, G1. Только начав движение из клетки A8, Робот остановится в ней же после выполнения программы. Ответ: 1,A8

Задача: Имеется исполнитель Кузнечик, который живет на числовой оси. Система команд Кузнечика: Вперед N (Кузнечик прыгает на N единиц вперед); Назад M (Кузнечик прыгает на M единиц назад). Переменные N и M могут принимать любые целые значения. Известно, что Кузнечик выполнил программу из 51 команды, в которой команд Назад 2 в 2 раза больше, чем команд Вперед 3, Других команд в программе не было, На какую одну команду можно заменить эту программу, чтобы Кузнечик оказался в той же точке, что и после выполнения программы?

Решение: Вычислим, сколько каких команд выполнил Кузнечик. Получаем: 51 / 3 = 17. Команд Вперед было 17, а Назад 2 было 34. Кузнечик прыгнул вперед на 17 ⋅ 3 = 51 единиц, а назад на 34 ⋅ 2 = 68. Тем самым он оказался на 68 - 51 = 17 единиц назад от первоначальной точки. Последовательность команд в алгоритме в данном случае не имеет значения. Ответ: Назад 17

Задача: Цепочка из трех бусин формируется по следующему правилу: на первом месте в цепочке стоит одна из бусин М, Н, О. На втором - одна из бусин Л, М, 0. На третьем месте - одна из бусин Л, М, 0, не стоящая в цепочке на первои или на втором месте.

Какая из следующих цепочек создана по этому правилу:

1) НОН 2) НОМ 3) МНЛ 4) МНО

Решение: Можно решать задачу, составляя все варианты цепочек, но эффективней решать методом исключений. Правилу первой буквы удовлетворяют все цепочки. В 3-ей и 4-ой цепочках нарушено правило второй буквы. В 1-ой цепочке нарушено правило третьей буквы. Ответ: 2

Задача: Цепочки символов (строки) создаются по следующему правилу.

Первая строка состоит из одного символа - цифры 1.

Каждая из последующих цепочек создается такими действиями: в очередную строку дважды записывается цепочка цифр из предыдущей строки (одна за другой, подряд), а в конец приписывается еще одно число - номер строки по порядку ( на i-ом шаге дописывается число i).

Вот первые 4 строки, созданные по этому правилу*

1) 1

2) 112

3) 1121123

4) 112112311211234

Какая цифра стоит в восьмой строке на 250-м месте (считая слева направо)?

Решение: Найдем длину восьмой строки, По условию длина каждой последующей строки увеличивается в 2 раза по сравнению с предыдущей плюс еще один символ. Длина строк составит:

1) 1

2) 1 ⋅ 2 + 1 =3

3) 3 ⋅ 2 + 1 = 7

4) 7 ⋅ 2 + 1 =15

5) 15 ⋅ 2 + 1 = 31

6) 31 ⋅ 2 = 1 = 63

7) 63 ⋅ 2 + 1 = 127

8) 127 ⋅ 2 + 1 = 255

Так как требуется найти 250-ую цифру, а всего в строке - 255, то искомая цифра шестая с конца. На каждом шаге к строке добавляется номер строки, поэтому последние 8 цифр будут выглядеть так: 12345678, Шестая цифра с конца - 3. Ответ: 3.

Задача: Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150. Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.

Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.

В конструкции

ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ

выполняется команда1 (если условие истинно) или команда2 (если условие ложно).

Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 68 идущих подряд цифр 8? В ответе запишите полученную строку.

НАЧАЛО
ПОКА нашлось (222) ИЛИ нашлось (888)
ЕСЛИ нашлось (222
ТО заменить (222, 8)
ИНАЧЕ заменить (888, 2)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ

Решение: Первые три шага цикла алгоритма заменят группу из 9-ти восьмерок на 222, а четвертый шаг заменит 222 на 8. Поэтому 7 групп по девять восьмерок заменяться на семь восьмерок и в итоге в строке их останется 7 + 68 - 9 ⋅ 7 = 12. Из этих 12-ти восьмерок девять опять будут заменены на одну восьмерку - останется в строке их четыре. Три восьмерки заменятся на двойку - получится 28. Ответ: 28

Задача: Два игрока играют в следующую игру:

Имеются три кучи камней, содержащих соответственно 1, 2, 3 камня. За один ход разрешается или утроить количества камней в какой-нибудь куче, или добавить в каждую из трех куч по 3 камня. Предполагается, что у каждого игрока имеется неограниченный запас камней.

Выигрывает тот игрок, после хода которого в одной из куч становится больше 20 камней или во всех трех кучах сумарно становится не менее 30 камней.

Игроки ходят по очереди. Выяснить, кто выигрывает при правильной игре - первый или второй игрок.

Решение: Для решения задачи составим дерево игры, что удобней сделать в виде таблицы. В первом столбце - начальная позиция, в остальных столбцах - возможные варианты ходов игроков.

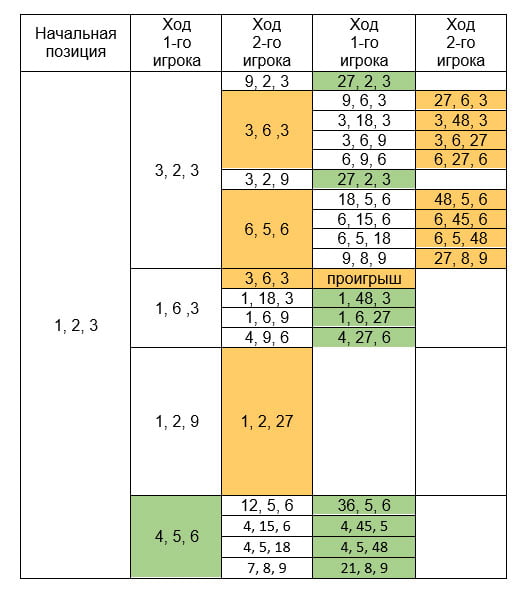
Таблица - дерево игры в камешки

Рассмотрим во втором столбце - четыре варианта хода 1-го игрока. Утроить количество камней в первой и во второй кучах 1-ый ирок не может, потому что при правильных ходах 2-го игрока (оранжевый фон ячейки таблицы) он проигрывает. Если он утроит количество камней в третьей куче, то он проиграет при первом же ходе 2-го игрока. 1-ый игрок выиграет при любом ответе 2-го игрока, если первым своим ходом добавит в каждую из куч по 3 камня. Ответ: 1-ый игрок

Задача: Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в четыре раза. Например, пусть в одной куче 6 камней, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (7, 9), (24, 9), (6, 10), (6, 36). Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.

Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 82. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 82 или больше камней.

В начальный момент в первой куче было 4 камня, во второй куче — S камней, 1 ≤ S ≤ 77.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по ней игрока, которые не являются для него безусловно выигрышными, то есть не гарантируют выигрыш независимо от игры противника.

а. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.

б. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:

в. Найдите минимальное значение S, при котором одновременно выполняются два условия:

Решение:

а. Так как минимальное значение количества камней, когда игра заканчивается, в обеих кучах равнв 82, а в первой уже 4, то во второй куче должно быть 78, чтобы игра окончилась за один ход Вани. Минимальное значение количества камней во второй куче должно быть равно 20, чтобы Ваня смог бы его учетверить для выигрыша. А минимальное количество камней во второй куче должно быть 5, чтобы Петя своим ходом, учетверив ее, смог бы достичь 20. Ответ: 5.

б. Чтобы Петя не смог бы выиграть за один ход, во второй куче должно быть не более 19 камней, потому что 20 камней - это минимальное количество камней, при котором можно выиграть одним ходом. Поэтому проверим позицию (4, 19). В этой позиции Пете достаточно для выигрыша положить в первую кучу один камень (5, 19), потому что при любом ходе Вани, следующим ходом Петя увеличивает в 4 раза количество камней во второй куче. Первое число 19.

Предположим, что в первой куче оказалось 16 камней после выигрышного хода Пети. Тогда во второй куче должно было бы быть 68 камня, как минимум. Следовательно, в начальной позиции во второй куче должно быть не более 16 камней, чтобы Ваня не смог бы выиграть первым ходом. Проверим начальную позицию (4, 16): Пете достаточно учетверить количество камней в первой куче, чтобы оставить Ване позицию (16, 16,). При любои ходе Вани, Петя увеличивает в 4 раза количество камней в большей куче и выигрывает. Второе число: 16.

в. В пункте б выяснилось, что позиция (4, 19) выигрышная для первого игрока, поэтому предположим, что нужная начальная выигрышная позиция для Вани (4, 18). После первого хода Пети могут возникнуть позиции: (5, 18), (16, 18), (4, 19), (4, 72). Представим дерево игры в виде таблицы:

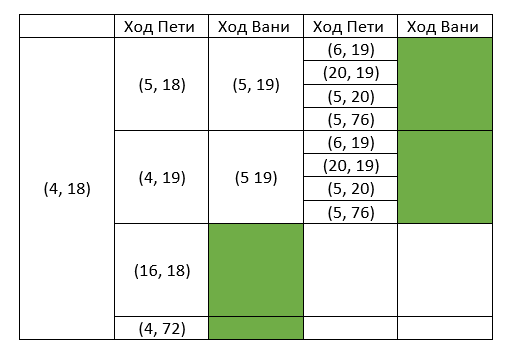
Таблица - дерево игры в камешки

Если предположить начальную позицию (4,15), то за 2 хода Ваня может не выиграть при правильной игре Пети (добавлять по одному камню в первую кучу). Ответ: 18.

 

Задачи для самостоятельного решения